Announcements
UPDATE August 2nd 2024: All charts have been replaced in Lesson 4 and Lesson 5. You will now have all the information required to complete the assignments for these lessons.
Welcome to Arithmancy 601
Before you enrol in this course, there are just a few things the Arithmancy team would like you to know.
- This course will involve some mathematical theory. Do not let this deter you, as we're always happy to assist with any questions you may have, whether they're about the general mathematical concepts, or Arithmancy-specific.
- We grade your assignments as quickly as we can but please do be patient.
- If you believe that there has been an error in the grading of your assignment, please send an owl to Professor Buchanan. We make mistakes sometimes, too. Just make sure to explain why you think there is an error, and include your assignment's ID number.
- If you have achieved 70% or higher in an assignment, you will not be able to retake it. Therefore, make sure you are happy with your work before submitting. If you are uncertain of something in the lesson, please ask for help before you complete the assignment.
Lesson 3) Setting Things in Order
Upon entering the classroom, you notice that Professor Buchanan is already there. He turns away from the board when he hears the students making their way inside and smiles brightly. “Find your seats, don’t be shy. Plenty of space at the front here,” he says, gesturing to the front row. “Make sure you can see the board clearly, please.”
Introduction
Welcome back to the Hall of Numbers. Today, we are going to cover the most basic operations that you’ll have to use throughout your entire career in Arithmancy - and for many other purposes, as the operations we will discuss today are the bread and butter of any type of calculation. As always, you will get the opportunity to apply what you have learnt after class, and there will be some optional homework for those of you who want an extra challenge today. Having said that, let’s begin!
Operations and Order of Operations
![]() First things first, let us discuss what an operation is. In its simplest terms, an operation is a mathematical process that takes a certain amount of values (also called ‘operands’) and creates a new number based on a specific rule (also called ‘operator’). There are many types of operations - and, in fact, nothing prevents you from inventing your own - but we tend to rely on some standard rules and symbols that are used by nearly every person, including Muggles. You have seen some of these in this class already: addition (+), subtraction (-), multiplication (*) and division (/) are some of the most classical operations we have in Arithmancy.
First things first, let us discuss what an operation is. In its simplest terms, an operation is a mathematical process that takes a certain amount of values (also called ‘operands’) and creates a new number based on a specific rule (also called ‘operator’). There are many types of operations - and, in fact, nothing prevents you from inventing your own - but we tend to rely on some standard rules and symbols that are used by nearly every person, including Muggles. You have seen some of these in this class already: addition (+), subtraction (-), multiplication (*) and division (/) are some of the most classical operations we have in Arithmancy.
We will be reviewing all of these operations shortly, but I’d like to discuss a very important concept first: the idea that operations must follow a specific order. Sometimes, operations will fight to use the same number. For example, in the expression 2 + 5 * 3, both 2 + 5 and 5 * 3 want to make use of the number five. Which operation should happen first?
This is why we have created standards on which operations should happen earlier. You might already know this rule through the abbreviation PEMDAS, or BODMAS, depending on where you were raised. PEMDAS stands for Parentheses, Exponents, Multiplication, Division, Addition and Subtraction, while BODMAS means Brackets, Orders, Division, Multiplication, Addition and Subtraction. They are meant to be a nifty memory device for you to remember what operation comes first.
If you are paying close attention, you might have noticed that PEMDAS lists multiplication before division, whereas BODMAS does the opposite. This might seem like a contradiction, but the truth is that multiplications and divisions are essentially the same operation; a multiplication is the same as the division by the number’s inverse. The same holds true for addition and subtraction: addition is just the inverse of subtraction, so it does not matter whether you do the former or the latter first.
You might have been taught that practical rule in the past, but I find that it might be useful if someone explained why operations follow that specific order. Let me cover this briefly before we move forward.
First, we have parentheses. Simply put, sometimes we want specific operations to happen earlier, and for that reason we need a tool that allows us to force these operations to happen. This is the purpose of parentheses - they allow us to do a “manual override” on all operations in case we want to give a special kind of instruction. Example: 6 + 2 * 3 = 6 + 6 = 12 , while (6 + 2) * 3 = 8 * 3 = 24.
Next, we have exponents. As we will study in our next class, exponents are nothing more than repeated multiplications. Changing a number with an exponent before solving for that exponent will impact all numbers inside that repeated multiplication, which would not be appropriate. Example: 2^3 = 2*2*2 = 8, but 1 + 1^3 = 1+ 1*1*1 = 2.
The next step is multiplication and division. Multiplications and divisions are just a series of repeated additions or the serial counting of terms that fit in a given addition (for example, 2 * 3 is the same as the repeated addition 2 + 2 + 2, in which two is added three times, whereas 6 / 3 is the same as two, since we can form the number six by adding the number three to itself two times). Just as above, changing one of the elements in the multiplication or division without calculating that operation means we’re messing up with all of the numbers packed inside the operation at the same time.
Lastly, we have addition and subtraction. Since these operations are the most basic ones, they don’t need to be unpacked before any other form of calculation. Essentially, addition and subtraction are pretty much spin-offs of counting - for example, when you add two to four, you are essentially counting two numbers forward from the starting point four, which lands you on six. Subtraction is the same, but in the opposite direction.
As stated before, there might be other operations that you need to work with, such as modular arithmetic, logarithms or absolute values. The trick is to identify what kind of operation is happening beneath the surface in order to identify what should be calculated first. We will revisit this point when talking about more complex operations in our next class.
Brief Review of the Four Basic Operations
 In spite of the fact that many of you have not formally studied Arithmancy or even Muggle mathematics in the past, I am quite convinced that you are aware about the four basic operations - namely, addition, subtraction, multiplication and division. Still, I figure that it’s best to err on the side of caution and provide a brief review of these four operations before we move on.
In spite of the fact that many of you have not formally studied Arithmancy or even Muggle mathematics in the past, I am quite convinced that you are aware about the four basic operations - namely, addition, subtraction, multiplication and division. Still, I figure that it’s best to err on the side of caution and provide a brief review of these four operations before we move on.
As we discussed earlier, addition and subtraction are two opposite operations that deal with counting. Addition increases the amount of a given number, while subtraction reduces that number. In both cases, zero is considered to be the neutral number for these operations: adding or subtracting zero does not change the first number, as you are not increasing or decreasing its quantity by any value.
In the specific case of addition, all numbers that will be joined together are called addends, whereas the final result of the addition is called the sum. Furthermore, there are three more relevant properties associated with this operation: addition is a commutative, associative and distributive operation.
Commutative means that it does not matter the order you add numbers to one another, you are going to get the same result. For example, 4 + 3 = 3 + 4. Furthermore, the associative property is also quite similar to the commutative one, as it states that you can add terms in whichever order you like when you have three or more addends. For example, if you have the expression 1 + 2 + 3, you may choose to add one to two first, followed by adding the resulting three to the other three, or you may choose to add two and three together, followed by adding the resulting five to the one. In both cases the final result is the same: the number six. In mathematical terms, 1 + 2 + 3 = 3 + 3 = 6 or 1 + 2 + 3 = 1 + 5 = 6.
Lastly, the distributive property states that when you multiply an addition of numbers, you may also multiply each individual number without changing the result. For example, assume that the number two multiplies the addition 3 + 5 - in other words, visualize the expression 2 * (3 + 5). Although I may solve the brackets first and get 2 * 8 = 16, I may also distribute the two as a multiplier for both elements of the sum. This nets the expression 2 * 3 + 2 * 5 = 6 + 10 = 16, providing the same value as above.
Subtraction, on the other hand, is neither commutative nor associative for a simple reason - while addition terms all increase the value, subtraction works in the opposite direction, fighting against the number that it intends to reduce. For that reason, 8 - 2 is different from 2 - 8, as swapping the terms changes the “strength” of each opponent, so to say. This is exactly why partial terms in subtraction have different names: the first number is the minuend, whereas the second number is the subtrahend. The final result of a subtraction is called the difference between both numbers.
However, we can use the distributive property when dealing with the multiplication of a subtraction. For example, take the expression 4 * (3 - 1). In this case, both solving the subtraction first and then calculating 4 * 2 = 8 as well as multiplying each term by four and then calculating the subtraction 12 - 4 = 8 would give the same result. This is because both multiplying the resultant difference between the numbers’ powers, as well as their base powers and then multiplying it by a given factor gives us the same product: the difference in their values scaled by the multiplying number.
Moving on to multiplication and division! Both of these operations refer to repeated additions - multiplication entails checking the final value of adding a given number to itself for a certain number of times, while division is all about finding the value that, if added to itself a given number of times, would give a target number as a result. Since we’ve already covered these definitions previously in today’s lesson, let us dive right into the properties of both of these operations.
The first thing you need to know is that, differently from addition and subtraction, one is the neutral number for multiplication and division. After all, if you’re adding a number to itself only one time or figuring out how many times a number fits into itself if you don’t break it down, the answer will always be the original number. Examples: 6 * 1 = 6, and 6 / 1 = 6.
Let’s move onto multiplication specifically, then. The initial terms for a multiplication are called factors, whereas the final result is called product. Some people also give specific numbers to the factors, calling the first one a multiplicand and the second one a multiplier; however, that distinction is not particularly necessary, for reasons we will cover shortly.
One thing that I want to mention before we proceed is that we need to be very careful with the symbols of the numbers we are multiplying. It’s obvious that when we multiply two positive numbers, the final result should also be positive - however, what if we multiply one positive and one negative number? What about two negative numbers?
The multiplication of a positive and a negative number generates a negative number. In order to better understand it, let’s think of a multiplication such as 10 * (-20) and try to use a physical analogy to make things simpler to understand: imagine that -20 represents you owing 20 Galleons to a friend. In this case, the multiplication 10 * (-20) can be interpreted as you owing 20 Galleons to a friend 10 times, which nets a total debt of 200 Galleons. Since debts are negative, this is the same as -200.
Now, what if we multiply two negative numbers? The final result of that multiplication will be positive instead, for very similar reasons. Again, let us consider a multiplication such as (-10) * (-20), and interpret -20 as owing 20 Galleons. However, this time, you are doing the opposite of owing your friend 10 times due to the negative sign in front of the 10: we may interpret this as your friend forgiving 10 debts of yours instead. In that case, forgiving 10 debts of 20 Galleons each means that you won’t need to pay 200 Galleons, making it a profit for you instead.
In case you need a visual reminder, here’s a nifty table with all types of multiplication patterns:
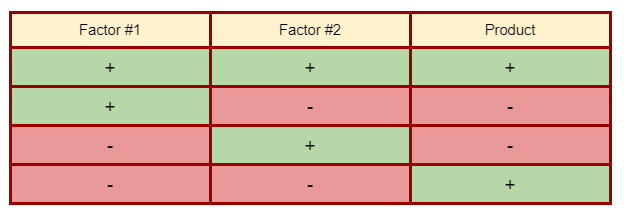
Multiplication is, just like addition, both a commutative and an associative operation. You will get equal results if you multiply 3 * 8 or 8 * 3, and there will be no difference based on what pair you multiply first if you’re calculating 4 * 5 * 9. Example: 4 * 5 * 9 = 20 * 9 = 180, 4 * 5 * 9 = 4 * 45 = 180, and 4 * 5 * 9 = 36 * 5 = 180.
The same is not true for division - which, like subtraction, has terms that possess different roles. The first number, also called dividend, indicates the final whole number that we want to test, whereas the second number, also called divisor, indicates the number we’re testing in order to see how many times it fits inside the dividend.
The interesting part of a division is that we might generate one or two numbers as a result. For divisions that deal only with integers, we might generate both a quotient (i.e., how many times the divisor fits in the dividend) and a remainder (i.e., the leftover number, smaller than the divisor, that couldn’t be used to fit one more copy of the divisor inside the dividend). However, remember that divisions may also be used to generate rational numbers instead - which means we can add decimal digits in order to indicate what part of a whole divisor could fit in the dividend’s leftovers.
One last thing I’d like to discuss is dividing a number by certain special values - more specifically, both itself and zero. Whenever we divide a number by itself, the final result will always be one - after all, a number can fit into itself only a single time. Conversely, dividing by zero provides an undefined result, as we can neither reach the desired dividend by adding zero to itself, no matter how many times we do that, nor add any number of zeroes to reach the desired dividend if the dividend happens to be zero itself. For that reason, we state that the result of a division by zero is undefined.
Digital Root of a Number
 Time for something new! The first new operation I would like to introduce is the so-called digital root, which takes any multi-digit number and converts it to a single-digit number between one and nine. This is done through a series of additions until you get to the final result.
Time for something new! The first new operation I would like to introduce is the so-called digital root, which takes any multi-digit number and converts it to a single-digit number between one and nine. This is done through a series of additions until you get to the final result.
For example, assume that you have the number 196425. In order to calculate the digital root of that number, we simply have to add all of the number’s digits together: 1 + 9 + 6 + 4 + 2 + 5 = 27. If you haven’t reached a single-digit number by the end of the process, repeat it once more: 2 + 7 = 9, meaning that the digital root of 196425 is nine.
There are some quite interesting properties in digital roots, including the fact that the number nine doesn’t change the digital root of a number. For example, consider the number 14, whose digital root is five. If I add any number of nines to it (for example, 919994999) and calculate the digital root for the number (9 + 1 + 9 + 9 + 9 + 4 + 9 + 9 + 9 = 68 → 6 + 8 = 14 → 1 + 4 = 5), you’ll see that I get to the same final result. This means that, if you have to calculate the digital root of any number that contains a nine, or digits that add up to nine, you can eliminate those digits to simplify your process. Going back to our 196425 example above, this number’s digital root is the same as the digital root to 162 (as nine can be eliminated and 4 + 5 add up to nine). This gives you the final sum 1 + 6 + 2 = 9, arriving at the same digital root as before.
Digital roots can also be used to validate different operations, such as complex multiplications and divisions. For example, imagine that someone tells you that 3572146 * 4231137 = 15174239110202. Without using a calculator or spending too much time replicating this multiplication, how can we prove that this multiplication is incorrect?
Using digital roots is a good way to do that. If we calculate the digital root of the first number, we can eliminate 3 + 6, 7 + 2 and 5 + 4 from the number, as all of these sets add up to nine. This means that the first number’s digital root is one. Applying the same process to the second number, we can remove 4 + 2 + 3 and 1 + 1 + 7, meaning that the second number’s digital root is three. Since 1 * 3 equals three, this means that the product to that multiplication will always have 3 as its digital root.
Let’s calculate the digital root of the product. If we eliminate (1 + 1 + 7), (5 + 4), 9, 0, 0 and (2 + 2 + 2 + 3) from its numbers, we get 11 as the last numbers that were not eliminated. Since the digital root of 11 is 1 + 1 = 2, this means that the multiplication above is incorrect.
Note that this system proves with no shadow of doubt that the result is incorrect when the digital roots don’t match, but it doesn’t mean that the result is definitely correct if the digital roots match! For example, even though the addition 23 + 19 = 51 matches our digital root test (as dr[23] = 5, dr[19] = 1 and dr[51] = 6), 23 + 19 actually adds up to 42 (which also has a digital root of 6). For that reason, you can’t say for certain that a calculation is correct if the digital roots match; you can only say for certain that a calculation is not correct if the digital roots don’t match.
The Modulo Operator
 At last, we shall cover the last type of operation inspired by the four basic operators. Our final topic for today’s lesson is the modulo operator.
At last, we shall cover the last type of operation inspired by the four basic operators. Our final topic for today’s lesson is the modulo operator.
If you’ll recall our discussion on division, you might remember that we may generate two numbers from dividing numbers - we may have the quotient, which is how many times the divisor fits completely inside the dividend, and the remainder, the leftover part that’s not big enough to fit the divisor once again inside the dividend. In simple terms, the modulo operator (represented by the symbol %) simply returns that remainder as the result of the operation.
It’s important to know that, by definition, the modulo of an operation will always be:
- a whole number
- smaller than the divisor
The second statement should be quite intuitive: if the modulo is larger than the divisor, that means the divisor could fit inside at least one more time inside it!
However, something that might not be as intuitive is the fact that we can calculate the modulo of a negative number. In that case, what we do is add the divisor to the dividend until we get a number between zero and the divisor. For example, if we were to calculate -3 % 4, we can add 4 to -3, netting a final result of one. Since one is between zero and four, that is the result of the modulo operation.
Closing
Both the digital root and the modulo operation will be very important for your Arithmancy studies, as they are generally used to extract, respectively, the properties of non single-digit numbers and the relative properties of two numbers when paired with one another. This topic will be covered in greater detail throughout your applied studies of Arithmancy.
Dismissed.

Original lesson written by Professor Vaylen Draekon
Improvements made by Professor Calum Buchanan
Image credits here, here, here and here
Enroll


